Table Of Content

My guess is that they all started the experiment at the same time - in this case, the first model would have been appropriate. The following crossover design, is based on two orthogonal Latin squares. We give the treatment, then we later observe the effects of the treatment. This is followed by a period of time, often called a washout period, to allow any effects to go away or dissipate. This is followed by a second treatment, followed by an equal period of time, then the second observation.
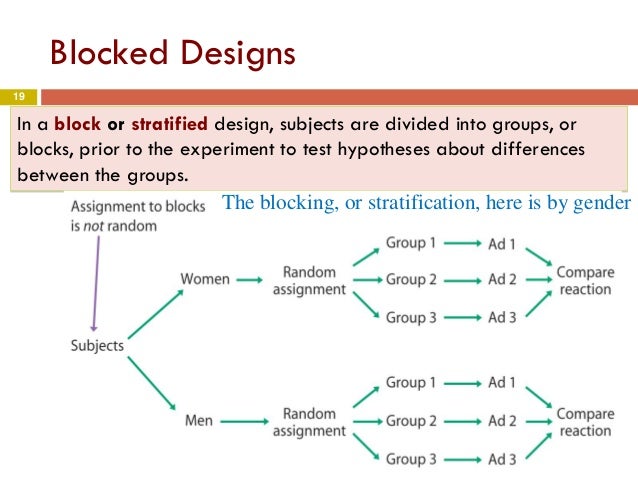
Other Aspects of the RCBD
Table 2 : Efficiency of RBD in comparison to CRD when plots were... - ResearchGate
Table 2 : Efficiency of RBD in comparison to CRD when plots were....
Posted: Fri, 08 Jun 2018 16:57:07 GMT [source]
Robust parameter design is widely used as an effective tool to reduce process variability by appropriate selection of control factors to make the process insensitive to noise. In this paper, we propose and study a method for selecting the optimal blocked robust parameter designs when some of the control-by-noise interactions are included in the model. We then discuss how to search for the best designs according to this method and present some results for designs of 8 and 16 runs.
Nuisance Variables vs. Lurking Variables
The degrees of freedom for error grows very rapidly when you replicate Latin squares. But usually if you are using a Latin Square then you are probably not worried too much about this error. The error is more dependent on the specific conditions that exist for performing the experiment. For instance, if the protocol is complicated and training the operators so they can conduct all four becomes an issue of resources then this might be a reason why you would bring these operators to three different factories. It depends on the conditions under which the experiment is going to be conducted.
Complete Block Designs
The row effect is the order of treatment, whether A is done first or second or whether B is done first or second. So, if we have 10 subjects we could label all 10 of the subjects as we have above, or we could label the subjects 1 and 2 nested in a square. This is similar to the situation where we have replicated Latin squares - in this case five reps of 2 × 2 Latin squares, just as was shown previously in Case 2. Consider a factory setting where you are producing a product with 4 operators and 4 machines.
Then, under the null hypothesis of no treatment effect, the ratio of the mean square for treatments to the error mean square is an F statistic that is used to test the hypothesis of equal treatment means. To conduct this experiment we assign the tips to an experimental unit; that is, to a test specimen (called a coupon), which is a piece of metal on which the tip is tested. The first \(F\)-test is based on the inter-block information about the treatment, and is in general (much) less powerful than the second \(F\)-test based on the intra-block information. As expected, the estimates are similar to those we found previously, but confidence intervals are substantially narrower due to the increase in precision.
Select appropriate blocking factors
If we choose one of the RCB Design Structures, Temperature effects are completely randomized at the Run level. Recipe is nested within temperature and has a different error structure than temperature, because each dough appears within each run. The contrasts looking at recipe and recipe by dough non-additivity (interaction) do not have run-to-run variability in them.
Analysis of BIBD's
A common choice for blocking mice is by litter, since sibling mice often show more similar responses as compared to mice from different litters (Perrin 2014). Litter sizes are typically in the range of 5–7 animals in mice (Watt 1934), which would easily allow us to select three mice from each litter for our experiment. In contrast to a randomized complete block design, we cannot increase the number of blocks to increase the replication. With two levels of Sex fixed, we instead need to increase the experiment size by using multiple mice of each sex for each drug. Since Sex and Drug are fixed, so is their interaction, and all fixed factors are tested against the same error term from (Mouse). Each treatment occurs only once per block, and the variations due to interactions and residuals are completely confounded.
A special case is the so-calledLatin Square design where we have two blockfactors and one treatment factor having \(g\) levels each (yes, all of them!).Hence, this is a very restrictive assumption. In a Latin Square design, eachtreatment (Latin letters) appears exactly once in each row and once ineach column. If we ignore the columns of a Latin Square designs, the rows form anRCBD; if we ignore the rows, the columns form an RCBD.
While such designs are commonly and successfully used, especially in smaller experiments, their application can often be unrealistic or impractical in many settings. Let’s start with the basic 22 factorial design to introduce the effective use of blocking into the 2k design (Table 1). Let’s assume that we need at least three replications for this particular experiment. If one batch can produce enough raw materials for only four samples (experimental units), only one replication can be made from one batch. Therefore, three batches will be required to complete the three full replications for the 22 basic factorial design (Table 2).
The blocking and confounding techniques in 2k factorial design of experiment is described in Video 1. In that sense, Latin Square designs are useful building blocksof more complex designs, see for example Kuehl (2000). In the most basic form, we assume that we do not have replicateswithin a block.
A similar exercise can be done to illustrate the confounded situation where the main effect, say A, is confounded with blocks. Again, since this is a bit nonstandard, we will need to generate a design in Minitab using the default settings and then edit the worksheet to create the confounding we desire and analyze it in GLM. When I have time to think it through, I'll update this further with the appropriate fancy names for those experiment designs. You are studying how bread dough and baking temperature affect the tastiness of bread.
The treatment factor is the design of the tip for the machine that determines the hardness of metal. By randomly assigning individuals to either the new diet or the standard diet, researchers can maximize the chances that the overall level of discipline of individuals between the two groups is roughly equal. By doing this, the variation within each block would be much lower compared to the variation among all individuals and we would be able to gain a better understanding of how the new diet affects weight loss while controlling for gender. Often in experiments, researchers are interested in understanding the relationship between an explanatory variable and a response variable.
As we shall see, Latin squares can be used as much as the RCBD in industrial experimentation as well as other experiments. When we have a single blocking factor available for our experiment we will try to utilize a randomized complete block design (RCBD). We also consider extensions when more than a single blocking factor exists which takes us to Latin Squares and their generalizations. When we can utilize these ideal designs, which have nice simple structure, the analysis is still very simple, and the designs are quite efficient in terms of power and reducing the error variation. The single design we looked at so far is the completely randomized design (CRD) where we only have a single factor. In the CRD setting we simply randomly assign the treatments to the available experimental units in our experiment.
Days of the week are not all the same, Monday is not always the best day of the week! Just like any other factor not included in the design you hope it is not important or you would have included it into the experiment in the first place. In this factory you have four machines and four operators to conduct your experiment. Use the animation below to see how this example of a typical treatment schedule pans out.
Notice that pressure is the treatment factor and batch is the block factor. The RCBD utilizes an additive model – one in which there is no interaction between treatments and blocks. The error term in a randomized complete block model reflects how the treatment effect varies from one block to another. The partitioning of the variation of the sum of squares and the corresponding partitioning of the degrees of freedom provides the basis for our orthogonal analysis of variance.
Get Involved With Block-Based WordPress Theme Experiments - WP Tavern
Get Involved With Block-Based WordPress Theme Experiments.
Posted: Wed, 15 Jan 2020 08:00:00 GMT [source]
Such interaction is likely caused by other biologically relevant factors that influence the effect of (some) treatments but that have not been accounted for in our experiment and analysis. It is important to distribute, as best one can,the different levelsof the treatment variables equally over the different levels of thecontrol variables. In case of substantial confounding, as when mostof the subjects receiving Placebo are Female and most of those receiving the Treatment are Male, it can become impossible to estimate the treatmenteffect. Similarly, when all Treatment subjects arein one batch and all Placebo in the other, batchand treatment are confounded and without a batch-independent referenceit is not possible to distinguish the treatment effect from a possiblebatch effect. Thus, it is important to account for control variablesin the experimental design and in the sample organization, and thiscan also be achieved using block randomization. The only systematic (non-random) differences in the observed responses result from differences between the treatments.


No comments:
Post a Comment