Table Of Content

Typical block factors are location (see example above), day (if an experiment isrun on multiple days), machine operator (if different operators are needed forthe experiment), subjects, etc. We can see in the table below that the other blocking factor, cow, is also highly significant. The numerator of the F-test, for the hypothesis you want to test, should be based on the adjusted SS's that is last in the sequence or is obtained from the adjusted sums of squares. That will be very close to what you would get using the approximate method we mentioned earlier. The general linear test is the most powerful test for this type of situation with unbalanced data.
2 - RCBD and RCBD's with Missing Data
Barberton, Ohio's Experiments With Urban Design - Bloomberg
Barberton, Ohio's Experiments With Urban Design.
Posted: Tue, 29 Aug 2017 07:00:00 GMT [source]
The experiment design looks similar to a factorial design of Chapter 6, but the interpretation of its analysis is rather different. Most importantly, while the factor Sex is fixed with only two possible levels, its levels are not randomly assigned to mice. This is reflected in the fact that Sex groups mice by an intrinsic property and hence belongs to the unit structure. In contrast, levels of Drug are randomly assigned to mice, and Drug therefore belongs to the treatment structure of the experiment. Proteomics has many aspects that oughtto be taken into accountwhen designing and planning experiments.
Mitigation of Batch Effects
Technically, this is called variously a split-plot design structure or a repeated-measures design structure. Here we have two pairs occurring together 2 times and the other four pairs occurring together 0 times. Crossover designs use the same experimental unit for multiple treatments.

Complete Block Designs
Instead of a single treatment factor, we can also have a factorial treatmentstructure within every block. We want to account for all three of the blocking factor sources of variation, and remove each of these sources of error from the experiment. For most of our examples, GLM will be a useful tool for analyzing and getting the analysis of variance summary table. Even if you are unsure whether your data are orthogonal, one way to check if you simply made a mistake in entering your data is by checking whether the sequential sums of squares agree with the adjusted sums of squares.
We discuss more sophisticated designs for blocking factorials that overcome this problem by using only a fraction of all treatment combinations per block in Chapter 9. We can think about creating a blocked design by starting from a completely randomized design and ‘splitting’ the experimental unit factor into a blocking and a nested (potentially new) unit factor. Two examples are shown in Figure 7.3, starting from the CRD (Figure 7.3A) randomly allocating drug treatments on mice.
What is a block in experimental design?
The idea of a latin square can be extended to more than two blocking factors; with three factors, such designs are called graeco-latin squares. We can also insist that each replicate forms a proper latin square in itself. That means we organize the columns in two groups of three as shown in the bottom of Figure 7.14B. In the diagram in Figure 7.15B, this is reflected by a new grouping factor (Rep) with two levels, in which the column factor (Litter) is nested.
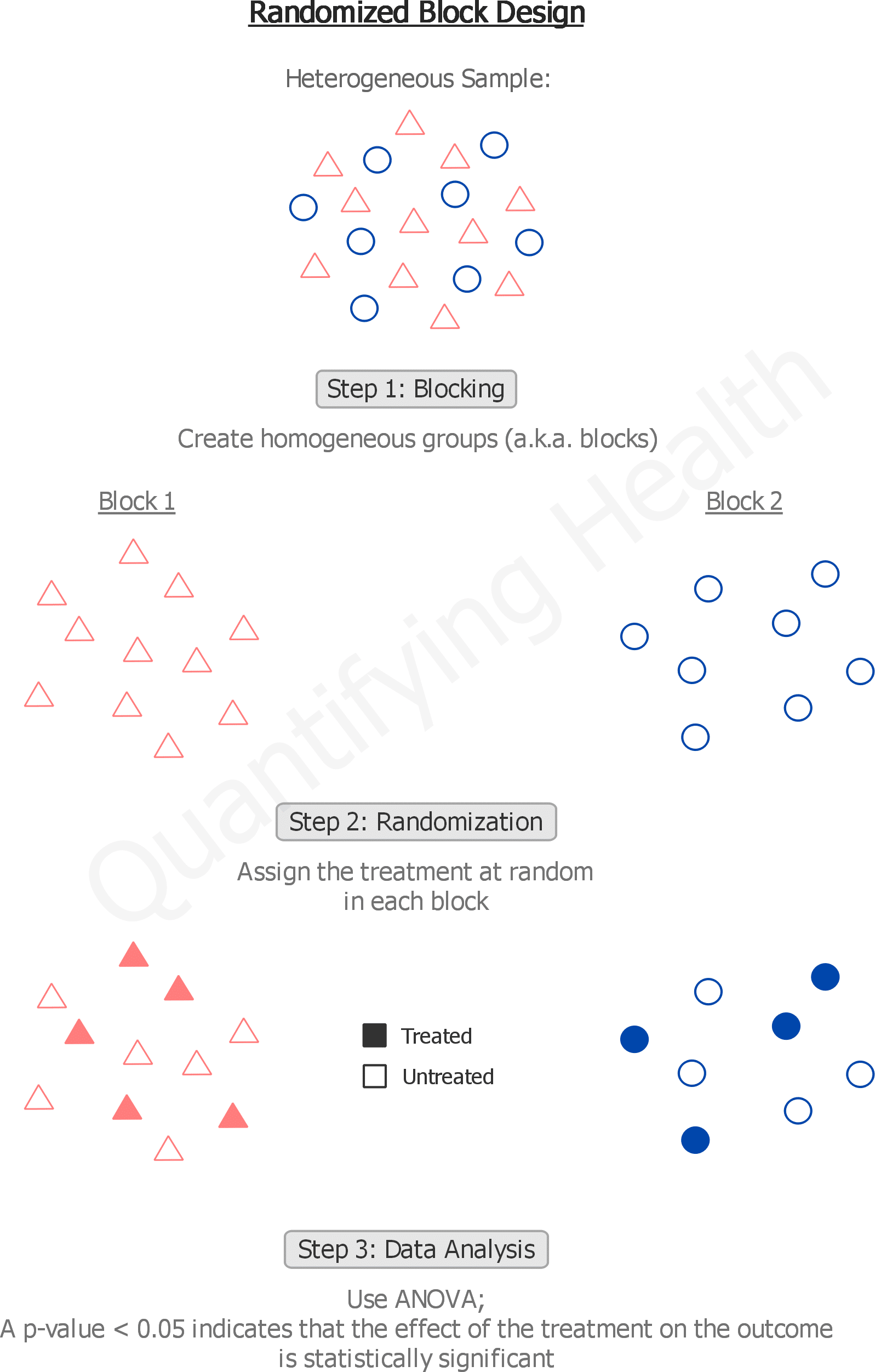
Sometimes several sources of variation are combined to define the block, so the block becomes an aggregate variable. Consider a scenario where we want to test various subjects with different treatments. The original use of the term block for removing a source of variation comes from agriculture. If the section of land contains a large number of plots, they will tend to be very variable - heterogeneous. First the individual observational units are split into blocks of observational units that have similar values for the key variables that you want to balance over.
The model y~drug+block, on the other hand, yields an entirely different ANOVA table and an incorrect \(F\)-test, as we discussed in Section 6.5. We cannot test the interaction factor and therefore require a non-statistical argument to justify ignoring the interaction. Since we have full control over which property we use for blocking the experimental units, we can often employ subject-matter knowledge to exclude interactions between our chosen blocking factor and the treatment factor. In our particular case, for example, it seems unlikely that the litter affects drugs differently, which justifies treating the litter-by-drug interaction as negligible. Several blocking factors can be combined in a design by nesting—allowing estimation of each blocking factor’s contribution to variance reduction—or crossing—allowing simultaneous removal of several independent sources of variation.
3 - The Latin Square Design
Think Strategically for Design of Experiments Success - BioProcess Insider
Think Strategically for Design of Experiments Success.
Posted: Tue, 01 Mar 2011 08:00:00 GMT [source]
Another purpose for using a multi-laboratory experiment is to broaden the inference for our experiment. For example, suppose each individual has a certain amount of innate discipline that they can draw upon to lose more weight. Since discipline is hard to measure, it’s not included as a blocking factor in the study but one way to control for it is to use randomization. In the previous example, gender was a known nuisance variable that researchers knew affected weight loss.
If you are simply replicating the experiment with the same row and column levels, you are in Case 1. If you are changing one or the other of the row or column factors, using different machines or operators, then you are in Case 2. If both of the block factors have levels that differ across the replicates, then you are in Case 3. The third case, where the replicates are different factories, can also provide a comparison of the factories. The fact that you are replicating Latin Squares does allow you to estimate some interactions that you can't estimate from a single Latin Square. If we added a treatment by factory interaction term, for instance, this would be a meaningful term in the model, and would inform the researcher whether the same protocol is best (or not) for all the factories.
The explanatory variables of interest are alsoreferred to as treatment variables, e.g., treatment, disease status,or tumor type. Where “i” is the index for replicates and “j” is the index for blocks within the replicates. In Design of Experiments, blocking involves recognizing uncontrolled factors in an experiment–for example, gender and age in a medical study–and ensuring as wide a spread as possible across these nuisance factors.
There are times where imputation is still helpful but in the case of a two-way or multiway ANOVA we generally will use the General Linear Model (GLM) and use the full and reduced model approach to do the appropriate test. Generally the unexplained error in the model will be larger, and therefore the test of the treatment effect less powerful. In some disciplines, each block is called an experiment (because a copy of the entire experiment is in the block) but in statistics, we call the block to be a replicate. This is a matter of scientific jargon, the design and analysis of the study is an RCBD in both cases.
In addition, considering the correlation between the image and prompt, AMFF-Net compares the semantic features from text encoder and image encoder to evaluate the text-to-image alignment. We carry out extensive experiments on three AGI quality assessment databases, and the experimental results show that our AMFF-Net obtains better performance than nine state-of-the-art blind IQA methods. The results of ablation experiments further demonstrate the effectiveness of the proposed multi-scale input strategy and AFF block. Blocked designs yield ANOVA results with multiple error strata, and only the lowest—within-block—stratum is typically used for analysis. Linear mixed models account for all information, and results might differ slightly from an ANOVA if the design is not fully balanced.


No comments:
Post a Comment